Modelling Terminal Velocity Vs. Ballistic Coefficient For Blunt Body Mars Entry Vehicles
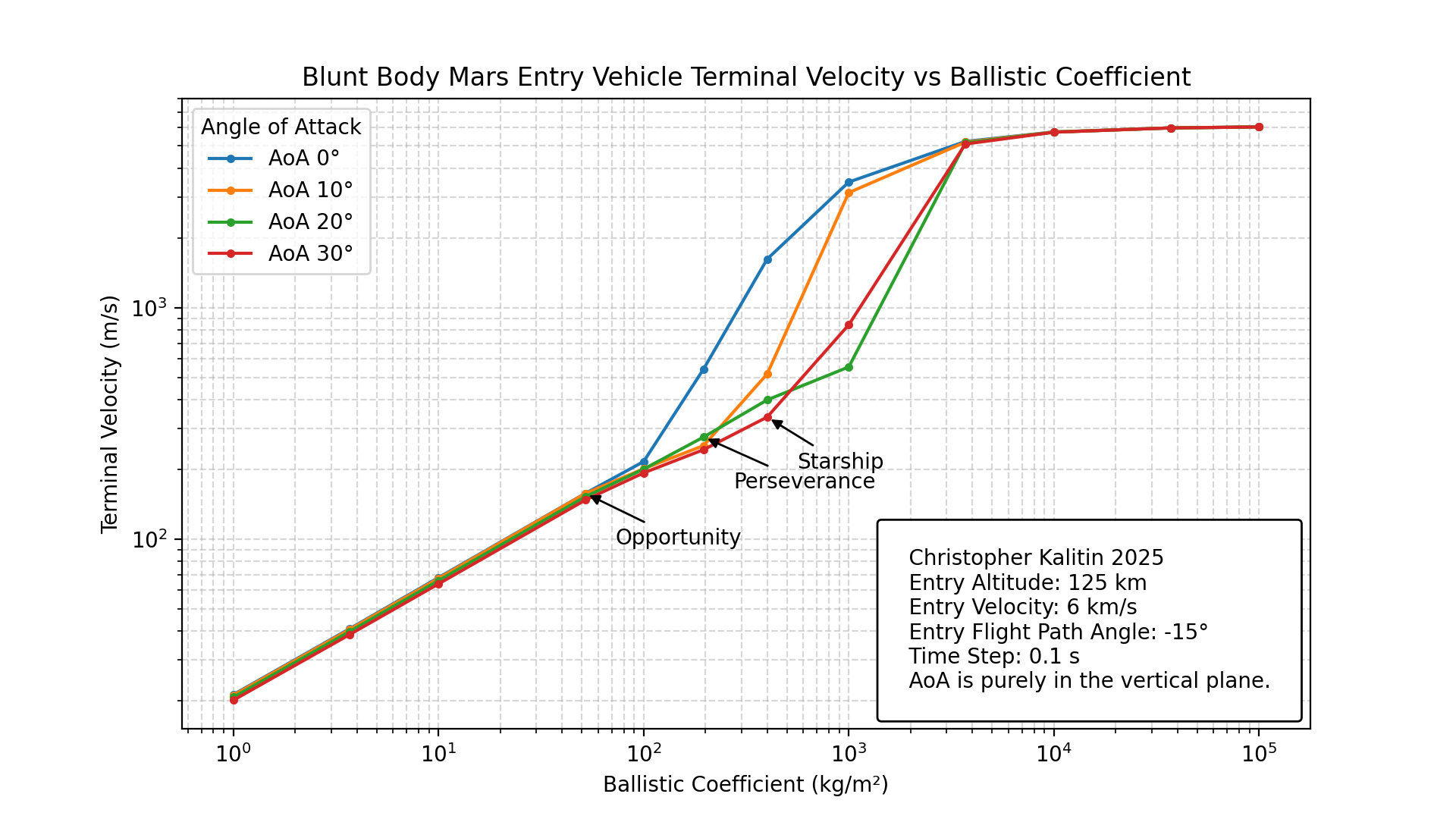
Log chart of Terminal Velocity vs. Ballistic Coefficient. If you want an efficient Mars Lander, better be on the left side of the mountain.
Notes
- Problem statement: To land on Mars you need a high ballistic coefficient
- How to land on Mars: Explain the phases of flight (illustrations and charts, explain the charts)
- Model summary (link other blog post)
- Chart summary (general trend and edge cases)
Ballistic Coefficient Points of Interest:
- The first divergence at BC=100 occurs because AoA=0 no longer reaches terminal velocity. (it’s not falling straight down).
- At BC=196 (Perseverance) AoA=20 is above AoA=10 because it’s falling straight down after a skip.
- At BC=1000, The great divergence occurs because at AoA=10 you get a collision and no skip. No skip!
- At BC=1000, AoA=30 is above AoA=20 because it again is falling straight down after a skip.
Structure:
- Introduction
- Companion Post
- Overview of Mars landing
- Max atmospheric decelleration
- Hence, min ballistic coefficient
- Casey Handmer / Starship / Blunt Body examples
- Model:
- First result (in the limit to zero, 0 vel - limit to inf, entry velocity)
- Then, Perseverance test and I realize AoA is extremely important
- AoA Chart with divergence at ~1000 BC
- First divergence at BC=100 because no terminal velocity, and higher AoA reaches v_t faster
- Then, Perseverance at BC=196 bc too high skip and BC=1000 AoA=30 > AoA=20